Interaction Curve

Introduction

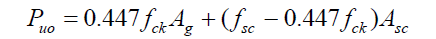
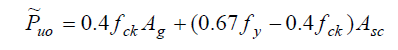
The interaction curve is a complete graphical representation of the design strength of a uniaxially eccentrically loaded column of given proportions. Each point on the curve corresponds to the design strength values of PuR and MuR associated with a specific eccentricity (e) of loading. The interaction curve defines the different (MuR, PuR) combinations for all possible eccentricities of loading 0 ≤ e < ∞. For design purposes, the calculations of MuR and PuR are based on the design stress-strain curves (including the partial safety factors), and the resulting interaction curve is sometimes referred to as the design interaction curve (which is different from the characteristic interaction curve).

In other words, the design interaction curve serves as a failure envelope. Of course, it must be appreciated that by the term safe , all that is implied is that the risk of failure is deemed by the Code to be acceptably low. It does not follow (as some designers are inclined to believe), that if the point (Mu, Pu) falls outside the failure envelope, the column will fail!

Salient Points on the Interaction Curve

The salient points, marked 1 to 5 on the interaction curve [Fig. 1.1] correspond to the failure strain profiles, marked 1 to 5

• The point 1 in Fig. 1.1 corresponds to the condition of axial loading with e = 0. For this case of pure axial compression, M1uR = 0 and PuR is denoted as Puo given by following equation

• The point 1'in Fig. 1.1 corresponds to the condition of axial loading with the mandatory minimum eccentricity emin [prescribed by the Code (Cl. 25.4 and 39.3)]. The corresponding ultimate resistance is approximately given by .

• The point 3 in Fig. 1.1 corresponds to the condition xu = D , i.e., e = eD. For e < eD, the entire section is under compression and the neutral axis is located outside the section (xu > D), with 0.002 < εcu < 0.0035. For e > eD, the NA is located within the section (xu < D) and εcu = 0.0035 at the highly compressed edge [Fig. 13.11]. Point 2 represents a general case, with the neutral axis outside the section (e < eD ).
• The point 4 in Fig. 13.12 corresponds to the balanced failure condition, with e = eb and xu = xu, b . The design strength values for this balanced failure condition are denoted as Pub and Mub. For PuR < Pub (i.e., e > eb), the mode of failure is called tension failure, as explained earlier. It may be noted that Mub is close to the maximum value of ultimate moment of resistance that the given section is capable of, and this value is higher than the ultimate moment resisting capacity Muo under pure flexure conditions [point 5 in Fig. 1.1].
• The point 5 in Fig. 1.1 corresponds to a pure bending condition (e = ∞, PuR = 0); the resulting ultimate moment of resistance is denoted Muo and the corresponding NA depth takes on a minimum value xu, min.

Analysis for Design Strength

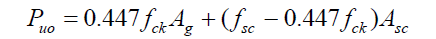
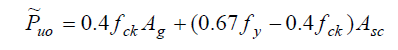
In this section, the detailed calculations for determining the design strength of a uniaxially eccentrically loaded column with a rectangular cross-section (b × D) is described in detail. The notation D denotes the ‘depth’ of the rectangular section in the plane of bending, i.e., either Dx or Dy, depending on whether bending occurs with respect to the major axis or minor axis, and the notation b denotes the breadth (width) of the section (in the perpendicular direction). The basic procedure for other cross-sectional shapes (including circular sections) is similar.

Generalised expressions for the resultant force in concrete (Cc) as well as its moment (Mc) with respect to the centroidal axis of bending may be derived as follows, based on Fig. 1.2

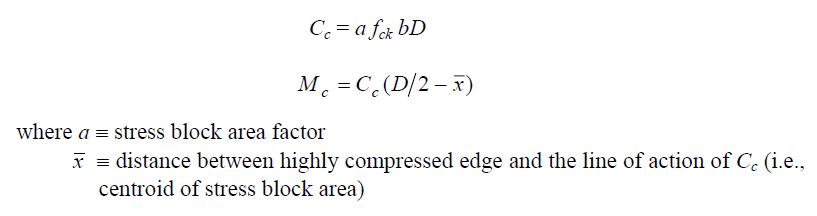
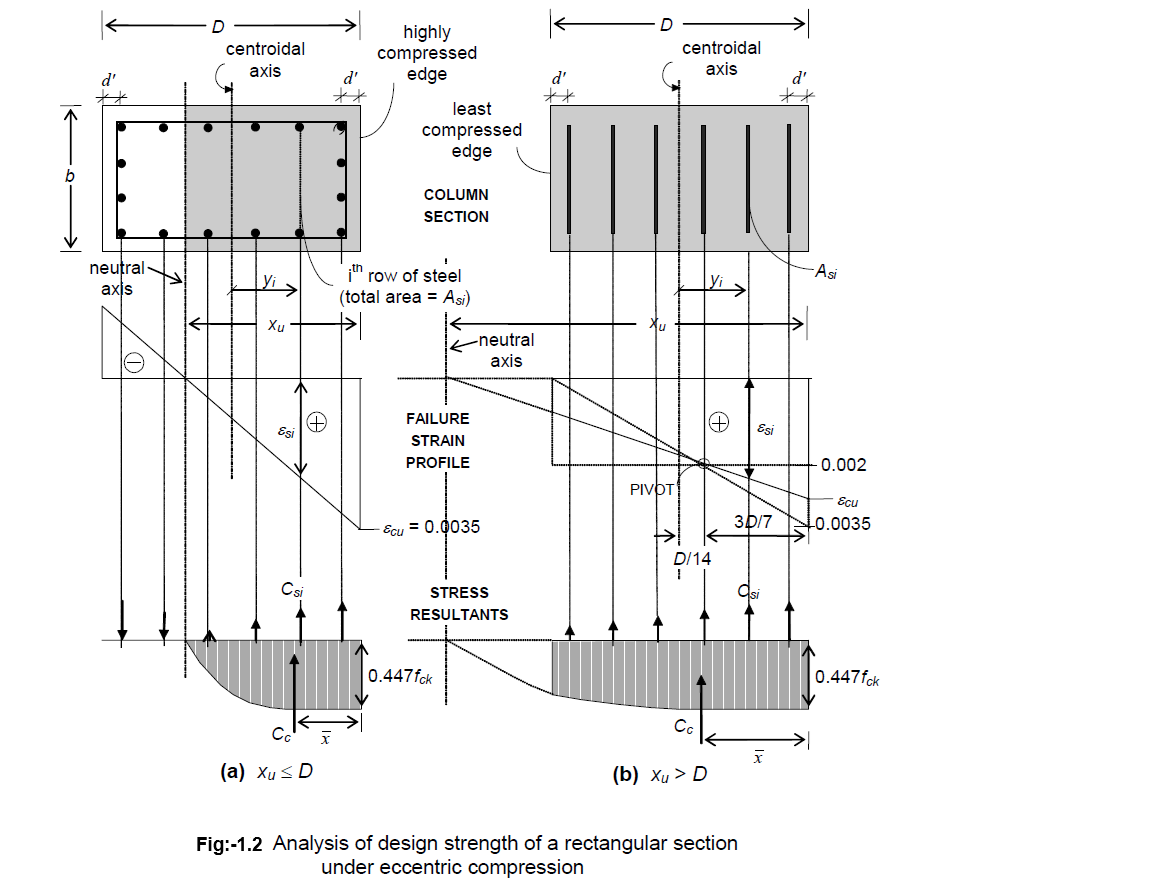
By means of simple integration, it is possible to derive expression for a and x for the case (a): xu ≤ D and for the case (b): xu > D

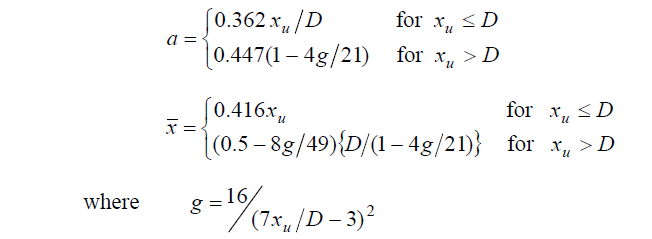
Similarly, the expressions for the resultant force in the steel (Cs) as well as its moment (Ms) with respect to the centroidal axis of bending is easily obtained as:

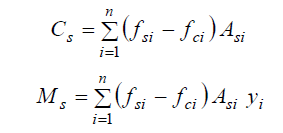
Prepared By Shiv Nath Mishra